La ley y el orden de la naturaleza: Fractales y Fibonacci
Matemáticas de la Naturaleza
Muchas cosas de la naturaleza son pura matemática aplicada, pero mucha gente no lo sabe y tal vez deberían! Es una forma siempre enriquecedora de ver y percibir la Naturaleza y las Matemáticas. De una manera o de otra, amplia la perspectiva de uno e incrementa el entendimiento y la consciencia de que todo en la Naturaleza en su esencia está relacionado... conectado. La Naturaleza ofrece muchas maravillosas soluciones a como hacer las cosas, porque ya se ha preocupado de todo desde hace miles de millones de años.
Así hay dos conceptos matemáticos que se pueden encontrar por todas partes en la Naturaleza:
la secuencia de Fibonacci y los Fractales.
La secuencia de Fibonacci
Fibonacci es el nombre de un matemático Italiano que en el año 1202 introdujo en Europa una secuencia de números muy especial, que ya se conocía en la India desde siglos antes.
La regla de esta secuencia es tan simple, que incluso los niños pueden entender y hasta 'inventarlo'. Empezando por 0 y 1, cada siguiente número es la suma de los dos anteriores:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144... y así hasta el infinito
Es una serie de números muy sencilla, pero muy utilizada por la Naturaleza.
Por ejemplo: casi siempre el número de pétalos de una flor son un número de esta serie y por la misma razón tenemos cinco dedos en las manos y los pies. Además de plantas y animales, se encuantra también en las grandes estructuras geológicas y astronómicas (quizás no en los propios números, sino por la espiral que deriva de ellos).
A pesar de (o tal vez gracias a) la sencillez de esta secuencia matemática, es una regla fundamental de todo lo que existe y puede llegar a describir fenómenos muy complejos.
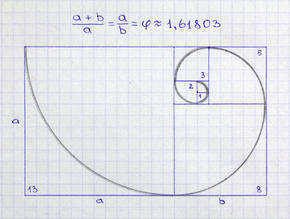
La forma más sencilla de poder "ver" de alguna manera esta secuencia, es dibujarlo en un papel con cuadritos.
De ahí sale, por un lado, lo que se considera el rectángulo más bello por la prooporción entre anchura y altura, y por otro lado esa espiral tan especial que se encuentra muchas veces en la naturaleza, desde las conchas y las tormentas hasta las galaxias.
Enseñar a los niños!
Dada su sencillez y su increíble repercusión, y a la vez su harmonía y belleza, no se explica porqué no se suele enseñar este conocimiento fundamental, tan pronto como cuando los niños hayan aprendido a contar y sumar. Porque se puede facilmente!
Adquirir este conocimiento tan hermoso, que relaciona directamente la Naturaleza y las Matemáticas de una forma tan sencilla, a una edad temprana aportaría seguramente un mayor entendimiento y apreciación por las dos cosas, para el resto de la vida y el futuro desarrollo del niño. Esta apreciación por parte de los futuros adultos sólo puede tener una repercusión positiva en toda la sociedad.
La Proporción Áurea
Directamente relacionado a la serie de Fibonacci está la Proproción Áurea.
Hay muchas formas para definir esta proporción, pero tal vez la más facil sea la de la división (áurea) de una línea:
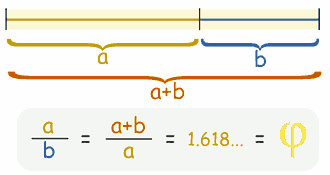
Dicho en palabras:
la relación entre la línea completa (a+b)
y la parte más larga de la división (a)
es igual a
la relación entre la parte larga (a)
y la parte corta (b)
esta relación es 1,618034....
Como es un número interminable para escribir, también se usa el signo phi: ϕ
Este número ϕ está un poco escondido en la serie de Fibonacci. Se revela al dividir cualquier número de la serie entre el número anterior:
5/3= 1,6666.....
8/5= 1,6
13/8 = 1,625
21/13 = 1.6153...
34/13= 1,6190...
55/34= 1,6176...
Como se puede observar, cuanto más alto los números consecutivos de la serie de Fibonacci, más se acerca el resultado a ese número ϕ
Rectángulos
La forma más fácil de "mostrar" lo especial de la Proporción Aurea se encuentra sencillamente en un rectángulo. Se considera que un rectángulo con estas proporciones es la más hermosa a la vista y se ha usado muchísimo en el arte y la arquitectura a lo largo de la historia en todas las culturas. Hoy día se usa entre otros para las tarjetas de crédito.
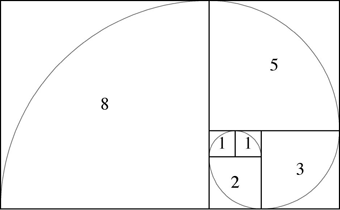
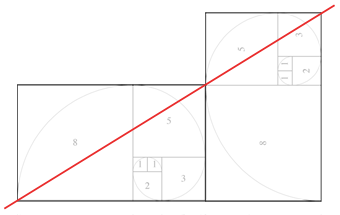
Más curioso todavía se hace con dos de estos rectángulos.
Sólo con la proporción phi: ϕ, se puede tener un rectángulo horizontal y otro vertical al lado, donde una diagonal cruza las tres esquinas. Esto se puede comprobar facilmente, con dos tarjetas de crédito (o del tipo que sea) y una regla.
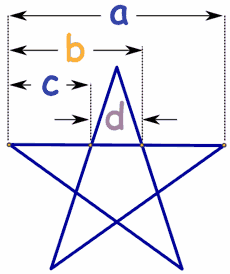
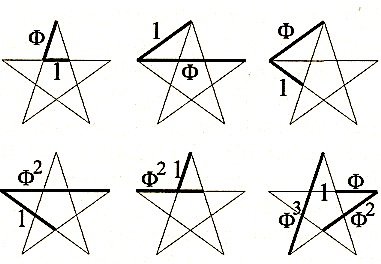
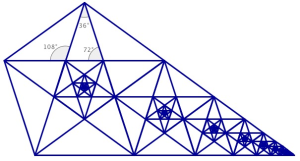
Pentagrama y pentágono
También en las formas geométricas con cinco lados iguales (la estrella pentagrama o el pentágono del centro) se encuentra la proporción phi: ϕ
Por ha sido utilizado como símbolo místico o mágico a lo largo de toda la historia humana.
La espiral
Finalmente la espiral derivada de estos números, como muestran el vídeo y los dibujos, también es especial. Es la espiral que siguen las conchas, los huracanes y las galaxias.
También la distribución de las semillas de un girasol (y muchas otras flores) siguen la forma de esta espiral. De hecho son dos grupos de espirales que van en direcciones opuestas, y el número de estos espirales también siempre corresponde a un número de la secuencia de Fibonacci, además dos números consecutivos!

Fractales
Para ponerlo de una forma simple, un fractal es una forma que se auto-replica (no necesariamente al 100% exacto) en cada escala en la que la miras, del mismo modo que las ramas de un árbol grande se pueden parecer a árboles más pequeños. Se encuentran fractales en las estructuras de las plantas o de nuestros pulmones, pero también en las de ríos y montañas.
la más simple...
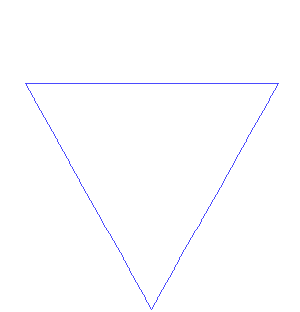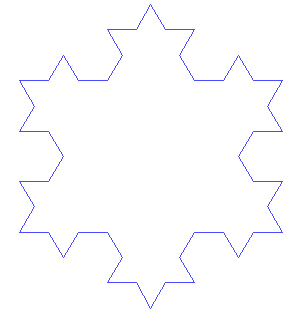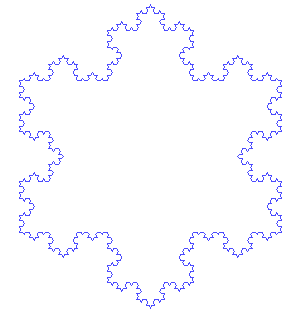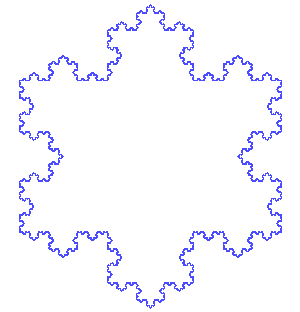
más elaborado...

Fractales de ordenador...



Fractales en la naturaleza...




Más enlaces Fibonacci y Fractales
- Log in to post comments
 English
English- Printer-friendly version


